Liste der Nachkommastellen von Pi
Die Nachkommastellen von Pi π...
Die Zahl von Nachkommastellen der Kreiszahl π ist unendlich und kann über verschiedenste Algorithmen berechnet werden.Auf dieser Seite finden Sie nun zunächst die erste Million von Nachkommastellen von Pi inkl. einer Downloadmöglichkeit als PDF.
Abschließend stellen wir Ihnen noch eine Möglichkeit vor diese selbst mit einem Java-Programm zu berechnen. Dazu sind grundlegende Java-Programmierkenntnisse erforderlich.
1 Million Nachkommastellen
Nachfolgend werden Ihnen nun die erste Million Nachkommastellen von Pi dargestellt. (Bitte haben Sie einen Moment Geduld. Das Laden der Liste kann ein paar Augenblicke dauern.)Und hier finden Sie die Download-Möglichkeit der ersten Million Nachkommastellen von Pi als PDF-Datei. (Was ist eine PDF-Datei?)
Berechnung über Java-Programm
Es gibt verschiedenste Wege die Kreiszahl π auf mathematische Art und Weise zu berechnen bzw. das Ganze dann auch entsprechend zu beweisen.Ein effizientes und geeignetes Berechnungsverfahren stellt die Abwandlung der Arcustangens Reihe dar, die wie folgt berechnet wird:
Diese Berechnung wurde in ein Java-Programm "gegossen" und für die Millionen Nachkommastellen entsprechend ausgeführt. Wenn Sie Programmierkenntnisse besitzen oder wissen, wie der folgende Java-Code zum Laufen gebrach werden kann, so können Sie die Klasse PiCalculator nutzen, um auf Basis der Arcustangens Reihe Nachkommastellen für π/Pi zu berechnen.
package PI;
import java.math.BigDecimal;
import java.math.RoundingMode;
public class PiCalculator {
private static final BigDecimal ZWEI = new BigDecimal("2");
private static final BigDecimal VIER = new BigDecimal("4");
private static final BigDecimal FUENF = new BigDecimal("5");
private static final BigDecimal ZWEIHUNDERT_NEUN_UND_DREISSIG = new BigDecimal(
"239");
public static void main(String[] args) {
System.out.println(pi(500000));
}
/**
* Berechnet PI mit einer entsprechenden Anzahl an Nachkommastellen:
*
* @param nachkommaStellen
* @return
*/
public static BigDecimal pi(int nachkommaStellen) {
return VIER.multiply(
(VIER.multiply(Arkusfunktion(FUENF, nachkommaStellen)))
.subtract(Arkusfunktion(ZWEIHUNDERT_NEUN_UND_DREISSIG,
nachkommaStellen))).setScale(nachkommaStellen,
RoundingMode.DOWN);
}
/*
* Arkusfunktion
*/
private static BigDecimal Arkusfunktion(BigDecimal x, int nachkommaStellen) {
nachkommaStellen += 10;
BigDecimal unity = BigDecimal.ONE.setScale(nachkommaStellen,
RoundingMode.DOWN);
BigDecimal sum = unity.divide(x, RoundingMode.DOWN);
BigDecimal xpower = new BigDecimal(sum.toString());
BigDecimal term = null;
boolean add = false;
for (BigDecimal n = new BigDecimal("3"); term == null
|| term.compareTo(BigDecimal.ZERO) != 0; n = n.add(ZWEI)) {
xpower = xpower.divide(x.pow(2), RoundingMode.DOWN);
term = xpower.divide(n, RoundingMode.DOWN);
sum = add ? sum.add(term) : sum.subtract(term);
add = !add;
}
return sum;
}
}





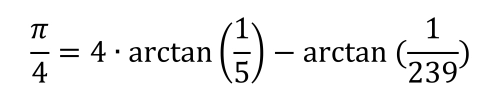
.jpg.webp)

